Tronc (geometria)

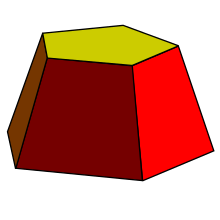
En geometria, el tronc és la part d'un sòlid, normalment d'un con o piràmide, que s'obté en tallar-lo amb dos plans paral·lels. Cadascuna de les interseccions amb els plans de tall és una base del tronc. L'eix, si existeix, és el del sòlid original. Un tronc és circular si les bases són circulars; d'altra banda, és recte si l'eix és perpendicular a les bases, i oblic en cas contrari.

Els cons i piràmides es poden entendre com a casos extrems de tronc en què un dels plans de tall és tangent al vèrtex.

Fórmules

El volum d'un tronc és la diferència entre el volum del sòlid original, menys la part exterior als plans de tall:

$V=\left|{\frac {h_{1}b_{1}}{3}}-{\frac {h_{2}B_{2}}{3}}\right|,$

on $h_{1}\,$ i $h_{2}\,$ són les distàncies des del vèrtex a les bases major i menor, sent $b_{1}\,$ i $B_{2}\,$ les àrees d'aquestes.

Tronc de piràmide hexagonal

Sigui $h\,$ l'alçada del tronc, és a dir la distància entre les bases, i tenint en compte que $h=\left|h_{1}-h_{2}\right|\,$ i que ${\frac {b_{1}}{B_{2}}}={\frac {h_{1}^{2}}{h_{2}^{2}}}$, s'obté una fórmula per al volum, on es relaciona aquest amb l'altura del tronc i l'àrea de les seves bases, mitjançant la mitjana heroniana.

$V={\frac {h}{3}}(b_{1}+{\sqrt {b_{1}B_{2}}}+B_{2})$

Tronc cònic

En particular, el volum d'un tronc cònic és:

$V={\frac {\pi h}{3}}(R_{1}^{2}+R_{1}R_{2}+R_{2}^{2})$

on $R_{1}\,$ i $R_{2}\,$ són els radis de les bases.

Tronc circular

Usant les definicions precedents, en el cas d'un con truncat, la fórmula es simplifica:

$V={\frac {\pi }{12}}hD_{1}^{2}\left(1-\left({\frac {D_{2}}{D_{1}}}\right)^{2}\right)$, on les D són els diàmetres de les bases.

De la mateixa manera:

$V={\frac {\pi }{12}}h\left(D_{1}^{2}-{\frac {D_{2}^{2}}{D_{1}/D_{2}}}\right)$

Vegeu també

• Tronc de con
• Escutoide

Enllaços externs

• Weisstein, Eric W., «Tronc piramidal» a MathWorld (en anglès).
• Weisstein, Eric W., «Tronc cònic» a MathWorld (en anglès).
• Models de paper de troncs de piràmides
• Problema sobre un tronc de con el·líptic i el seu volum

Viccionari